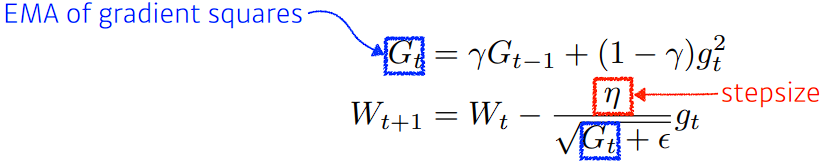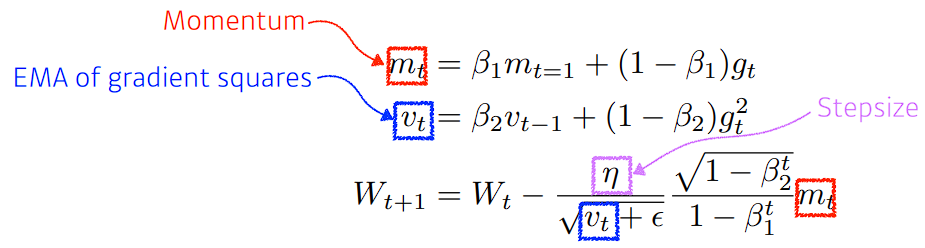Deep Learning Optimization

딥러닝에서의 최적화(Optimization)란 무엇일까?

단순하게 생각하면
랜덤으로 초기화된 모델의 weight들을
Gradient Descent를 통해 cost를 최소화하는 방향으로 변화시키는 것
이라고 답변할 수 있을 것이다.

하지만, 그 과정에서 고민하고 확인해야 할 것이 무엇이 있는지, 이를 위해 체크하면 좋을 것들에 대해 정리하고자 한다.

일반화(Generalization)에 대하여

최적화의 목표 중 하나는, 일반화 성능을 높이는 것이라 할 수 있다.

일반화 성능이란 무엇인가?

일반화 성능을 높이면 무조건 좋은건가?
일반화란 어떤 의미일까?

학습을 시키면 모델의 weight들이 training set의 cost를 최소화하는 방향으로 업데이트 된다.
계속 학습을 시키게 되면 점점 더 잘 맞추게 된다.
단, 일정 수준을 넘어버리면 training set에 과적합되어 test set에 대해선 잘 맞추지 못하는 모습을 보인다.
^{reference. 모두에게 너무나 익숙한 그 그림}

학습 데이터에 너무 맞추는 것도 아니고, 너무 못 맞추는 것도 아니고.
그 중간 어딘가가 가장 좋은(Balanced) 지점이라 할 수 있다.

하지만 이는 너무 이론적인 말이다.
실제 문제에서 항상 똑같이 적용할 수 있다고 할 수는 없다.

실제 풀고자 하는 문제의 타겟은
저 급격하게 변하는 모양새의 오버피팅된 모습일 수도 있고,
아예 다른 형태일 수도 있다.

우리가 가정하고 있는 것은
데이터가 학습하고자 하는 어떤 목적에서 발생된
구조적인 형태를 가지고 있을 것이라고 기대 뿐이다.

이 부분은 디테일한 분석을 통해 데이터에 대해 깊게 이해하고,
적절하게 문제를 정의하는 것이 가장 중요하다고 생각된다.

일반화된 지점을 어떻게 확인할까?

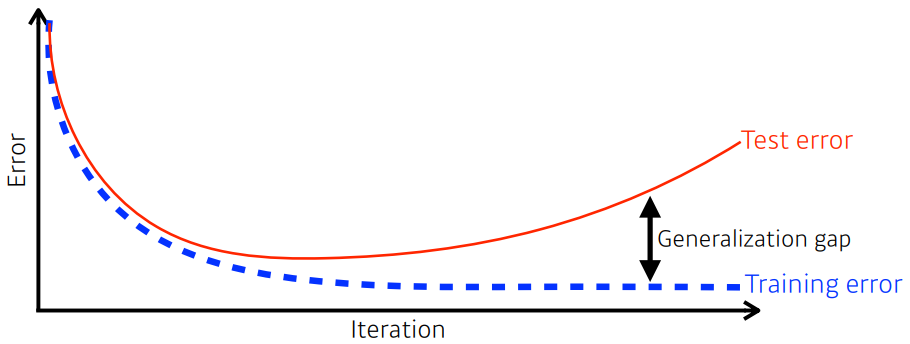
test error와 training error의 차이를 통해 얻는 일반화 갭의 상태를 보고 결정할 수 있다.
단, 이를 통해서는 이 모델의 성능이 학습 성능이랑 비슷할 것이란 사실만 알 수 있다.
학습 데이터에 대해 성능이 좋지 않으면_{(학습을 덜 했거나, 데이터에 노이즈가 너무 많이 껴 있거나, 데이터와 맞지 않는 모델을 사용했거나 등등..)}, 일반화 갭이 작다고 해서 잘 학습되었다고 할 수는 없다.

• 일반화 성능이 좋다 != 테스트 데이터 성능이 좋을 것이다
• 일반화 성능이 좋다 == 테스트 데이터 성능이 학습 데이터 성능과 비슷할 것이다

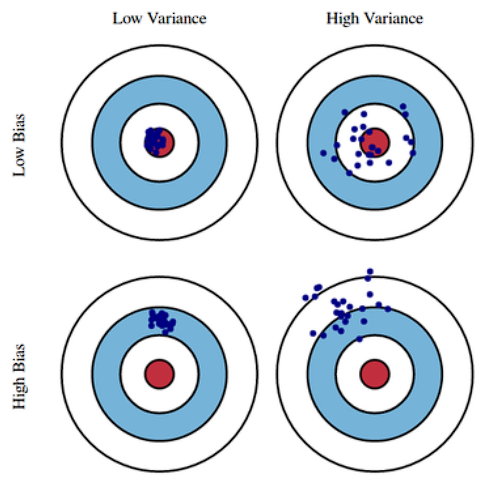
모델의 성능에 대한 Bias와 Variance

모델의 파라미터(weight, bias 등)를 말하는 것이 아님에 유의
사격 시 탄착군과 비슷한 개념으로 생각할 수 있다.

모델의 성능에 대한 Bias

비슷한 입력에 대해서 True Target에 얼마나 접근하는가.

• bias가 낮다
  • 출력이 많이 분산 되더라도 평균적으로 True Target에 접근하는 경우
• bias가 높다
  • True Target에 대해 평균적으로 많이 벗어나는 경우

모델의 성능에 대한 Variance

비슷한 입력을 넣었을 때 출력이 얼마나 일관적으로 나오는가

• variance가 낮다
  • 간단한 모델이 이런 경우가 많을 것이다. 비슷한 입력에 대해 둔감한 변화를 보인다.
• variance가 높다
  • 비슷한 입력에 출력이 많이 달라진다. overfitting이 생길 가능성이 높아진다.

Bias and Variance Trade-off

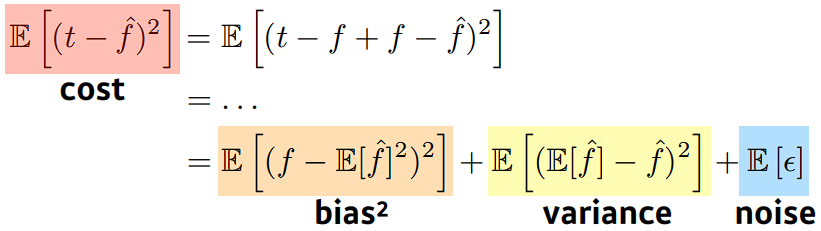
노이즈가 학습 데이터에 노이즈가 껴 있다고 가정했을 때,
cost는 bias, variance, noise 3가지 파트로 이루어져 있다.

데이터의 cost를 minimize하는 것은 사실 각각을 minimize 하는 것이 아니다.

따라서, 하나가 줄어들면 하나가 커질 수 밖에 없고,
각 파트는 trade-off의 관계에 있다.

이는 모델의 성능에 대한 이론적 한계(fundamental limit)가 된다.

Gradient Descent에 대하여

학습시 활용하는 데이터 수(배치 사이즈)에 따른 분류

• Stocastic Gradient Descent
  • 한 개 sample씩만 활용
• Mini-batch Gradient Descent
  • 일부 sample을 모아 data를 subset으로 만들어 활용
• Batch Gradient Descent
  • 전체 데이터를 한번에 활용

배치 사이즈를 얼마로 잡아야 할까?

1개를 쓰면 너무 오래걸리고,
너무 많이 넣으면 GPU 메모리가 터지고,
적절한 수를 찾아야 한다.
^{논문: On Large-Batch Training for Deep Learning}

• 라지 배치사이즈를 사용하면 sharp minimum에 도착한다.
• sharp minimum에서는 testing function에서 조금만 멀어져도 잘 동작하지 않을 수 있다.(위 이미지의 보라색 선 참고)
• flat minimum에 도착하면 testing function에서 조금 멀어져도 괜찮은 성능을 기대할 수 있다.
• flat minimum에 도착하면 일반화 성능이 높아진다.
• sharp minimum보다는 flat minimum에 도착하는 것이 더 좋다.
• 배치 사이즈를 작게 쓰는게 일반적으로 좋다.

Gradient Desent Methods

똑같이 Gradient Information만 이용해서
어떻게 더 좋은 성능, 혹은 더 빠른 학습을 시킬 수 있을까? 에 대한 고민

자동으로 미분을 해 주는 딥러닝 프레임워크의 핵심으로,
Optimizer로 구현되어 있고 적절한 것을 골라 활용할 수 있다.

각각이 왜 제안이 되었고, 어떤 성질이 있는지를 알아두면 좋다.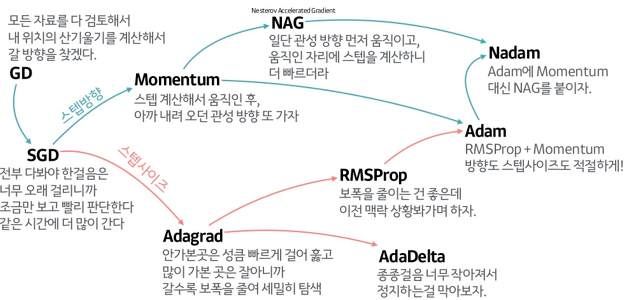
^reference

• (Stocastic) Gradient Descent
  • 가장 기본적인 GD를 활용하는 방법.
  • Gradient를 구해서 learning rate만큼 빼준다.
  • lr을 적절히 잡아주는게 매우 어렵다.
• Momentum
  • 관성
  • 이전 배치에서 어느 방향으로 흘렀는지에 대한 정보를 활용하자.
  • 한번 흘렀으면, 다음번에 조금 다르게 흘러도 이쪽 방향으로 흐르던 정보를 이어가자.
  • momentum과 현재 Gradient를 합친 Accumulation Gradient를 사용
  • 한번 흐른 Gradient를 유지시켜줘서 Gradient가 왔다갔다해도 잘 훈련되도록 도와준다.
• NAG(Nestrov Accelerated Gradient)
  • Gradient를 계산할 때 Lookahead Gradient를 계산한다.
  • 현재 자리에서 한번 가 보고 간 자리에서 계산한 것으로 Accumulation.
  • 위의 방법들은 local minima에 왔다갔다 하며 닿지 못하는 모습을 보일 수 있는데, 이를 봉우리에 닿도록 도와줄 수 있다.
• Adagrad (Adaptive grad)
  • 파라미터가 지금까지 얼마나 변해왔는지를 확인한다.
  • 많이 변한 파라미터는 적게 변화시키고, 적게 변한 파라미터는 많이 변화시킨다.
  • adaptive lr을 활용하게 된다.
  • G가 계속 커지기 때문에 G가 무한대로 갈 수록 점차 학습이 멈추게 되는 문제가 있다.
    
• Adadelta
  • G가 계속 커지는 현상을 막겠다.
  • 타임스탬프 t를 윈도우 사이즈 만큼의 그래디언트 변화를 보겠다
  • 이전 t개 동안의 G를 들고 있어야 된다.
  • 파라미터가 커지면 힘들다. (파라미터 수 * t의 공간 필요)
  • lr이 없다.
• RMSprop
  • 논문을 통해 제안된 것은 아니고, Geoff Hinton이 강의에서 이러니까 잘 되더라 한게 레퍼런스(…)
  • Adagrad에서 G를 구할 때 그냥 gradient square를 더하는 것이 아니라, exponential moving average를 더해 준다.
  • stepsize(η)를 사용한다.
    
• Adam (Adaptive Moment Estimation)
  • 일반적으로 가장 무난하게 사용.
  • RMSprop을 함과 동시에, 모멘텀을 같이 활용
  • β1 : 모멘텀을 얼마나 유지시키는지
  • β2 : gradient squares에 대한 EMA 정보
  • η : learning rate
  • ε : div by zero를 막기 위한 파라미터지만, 이 값을 잘 바꿔주는것도 실질적으론 중요하다
    

Regularization. 규제

학습을 방해하는게 목적이다.

학습을 방해함으로써 얻는 이점은
학습 데이터에서 뿐만 아니라
테스트 데이터에 대해서도 잘 동작하도록 하기 위함이다.

• Early stopping
  • loss 상황을 계속 보면서 일찍 학습을 멈추자.
  • 단, 학습을 멈출 때 test data를 활용하면 cheating이다.
  • 보통 validation error를 이용.
• Parameter norm penalty
  • 네트워크 파라미터가 너무 커지지 않도록 한다.
  • 이왕이면 네트워크 weight가 작은 것이 좋다.
  • 뉴럴넷이 만드는 함수의 공간(function space)을 최대한 부드러운 형태로 만들자.
    • weight가 작으면 function space가 부드러워진다.
    • 부드러운 함수일 수록 일반화 성능이 높을 것이다..! 라는 기대
• Data augmentation
  • 뉴럴넷에서 가장 중요한 것 중 하나.
  • 데이터가 적으면, DL보다 일반적인 ML방법론이 더 좋다.
  • 데이터가 많아지면, 많은 데이터에 대한 표현력이 ML방법론에선 부족하다.
    • 따라서 DL방법론의 성능이 더 좋아진다.
  • 단, 데이터를 변화시킴에도 정답이 변화하지 않는 수준에서 변화를 시킨다.
• Noise robustness
  • 사실 왜 잘되는지 아직 의문이 있긴 하다…ㅋㅋ(완전히 해석되지 않았다)
  • 입력 데이터에 noise를 넣는 것은 Data augmentation의 일부로 생각할 수도 있다.
  • 학습시킬 때 노이즈를 웨이트에 넣어줘도(weight를 흔들어도) 좋을 수 있다…
• Label Smoothing
  • 다른 Label의 샘플을 뽑아서 데이터와 라벨을 섞어준다.
  • 왜 잘 될까,,,?
    • 결국, 데이터들이 있는 공간 속에서 Decision Boundary를 찾는게 목표.
    • 이 경계를 부드럽게 만들어 주는 효과.
  • ex. mixup, cutmix
    
    ^{CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features}
• Dropout
  • 뉴럴넷의 weight를 랜덤하게 0으로 바꿔준다.
  • 각각의 뉴런들이 좀 더 robust한 feature를 잡을 수 있다라고 해석을 한다.. (수학적으로 증명된 것은 아님.)
  • 서로 다른 N개의 신경망을 앙상블하는 형태라 표현하기도 한다.
  • 일반적으로 쓰면 성능이 많이 올라가는 효과를 보인다.
• Batch normalization
  • 논란이 참 많다..ㅋㅋ(완전히 해석되지 않았다)
  • 내가 적용하고자 하는 BN 레이어의 통계량을 정규화.
  • 레이어 단 입력의 각각의 값들에 대하여 평균이 0인 정규분포로 만들어버린다.
  • 대부분의 경우 성능이 많이 올라간다… 성능을 올리는 것이 목표라면 활용하는게 좋다.
  • 이 글에 매우 잘 정리되어 있다.