Deep Learning 기본

딥러닝의 중요 요소

• 학습을 시킬 데이터(Data)
• 학습할 모델(Model)
• 학습시키기 위한 손실 함수(Loss)
• 손실을 최소화하는 최적화 알고리즘(Optimization Algorithm)

여러 차원의 벡터 공간과 선형 변환

• 세상이 선형으로만 이루어져있지 않다. _{1차원에서 1차원으로 가는 변환만을 찾지 않는다.}
• N차원에서 M차원으로 가는 모델을 찾고 싶을 수 있다.
• 행렬을 이용해 N차원에서 M차원으로 가는 mapping을 정의(affine transform)
• y = W^Tx + b _{(W와 b는 행렬과 벡터)}
• 행렬을 곱한다 == 두 vector space간의 변환
• 선형성을 가지는 변환이 있을 때, 그 변환은 항상 행렬로 표현된다
• 행렬을 찾겠다 == 두 다른 차원 사이에 선형 변환을 찾겠다
  

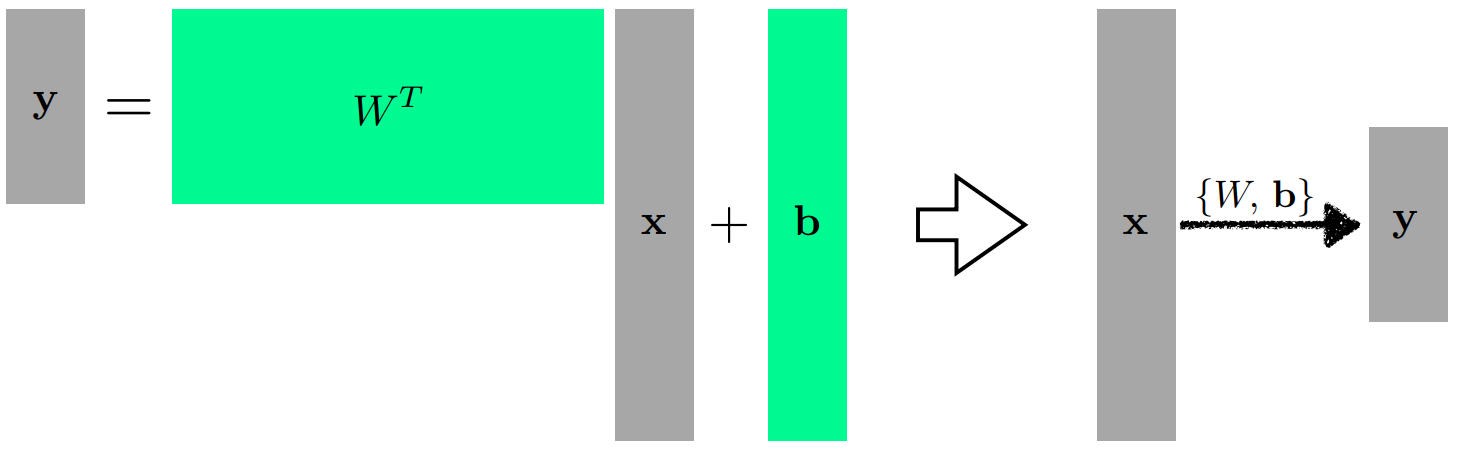
^{x와 y. 다른 차원의 두 벡터를 W 행렬을 통해 변환시켰다.}

Activation Function의 사용

• 핵심은, 모델이 최대한 많은 상황을 표현하도록 하는 것이다
• 네트워크를 깊게(deep) 쌓으려면?
  • 중간에 hidden vector들을 획득 후 목표 벡터를 획득하는 방법이 있다
  • 단, 이는 단순히 행렬들의 곱(선형 결합)에 불과하다
  • 선형 결합은, 아무리 깊어져도 한단짜리와 표현력이 같다
  • 즉, 단순한 선형 결합(linear transform)으로는 한계를 가진다
• mapping이 표현할 수 있는 표현력을 극대화하기 위해서는?
  • 비선형 결합(nonlinear transform)을 활용한다
  • 비선형 결합을 거친 후의 선형 변환을 n번 반복하여 더 많은 표현력을 얻을 수 있다
• 어떤 Activation Function이 제일 좋은가?
  • 사실, 어떤게 제일 좋을 지는 모른다.
  • 문제마다 다르고, 상황마다 다르다.
  • 각 활성 함수의 특징을 이해하고 문제에 활용하는 것이 좋다.

Loss Function에 대하여

• 입력이 주어졌을 때 출력값과, 목표의 차이를 정의
• 이를 최소화하는 것이 목표
• 이것이 항상 우리의 목적을 완성하지는 않는다
  • 항상 도움이 되지는 않을 수도 있다.
  • MSE가 선형 회귀에서 최적인가?
    • 제곱이 아니라 절댓값이나 네제곱을 활용해도 목표를 0으로 만드는 것은 같다.
    • 하지만, outlier가 있을 경우 큰 영향을 받게 된다.
    • 이렇듯, 어떻게 활용하는가에 따라 성질이 조금 달라진다.
  • cross entropy가 분류 문제 해결에 최적인가?
    • 분류를 잘 하는 관점에서는 결국 다른 값들 대비 높기만 하면 되는데?
    • 다만 이를 수학적으로 표현하기 까다로우니 활용하는 것일 뿐.
  • 확실하지 않은 확률 정보(uncertanty)를 같이 찾고 싶을 때는?
    • probalistic loss function을 활용하여 likelihood를 최대화 하는 방향으로..
• 이게 왜 우리가 원하는 결과를 얻어낼 수 있는지? 에 대한 이야기를 할 수 있어야 한다
• loss function이 어떤 의미를 가지고 있는지 생각하자